4.0 소개
가스 터빈 성능의 모든 측면에서 무차원, 준 차원, 참조 및 스케일링 매개 변수 그룹의 중요성은 아무리 강조해도 지나치지 않습니다. 매개 변수 그룹 간 관계의 형태를 이해하고 기억하면 주변 조건의 변화, 엔진 스케일링, 작동 유체 변화 등의 성능 영향과 관련하여 '현장에서' 판단할 수 있습니다. 모든 가스 터빈 성능 계산은 다음과 같이 두 가지 주요 방법으로 사용되는 매개 변수 그룹에 어느 정도 의존합니다:
(1) 구성 요소 특성의 엄격한 표현
(2) 전반적인 엔진 정상 상태 및 과도 성능에 대한 1차 근사치
본 장에서는 주요 매개변수 그룹에 대한 표 형식의 빠른 참조를 제공하면서 그에 대한 배경을 설명합니다. 이와 같은 그룹의 적용에 대해서는 이후 장에서 구성요소, 설계 외 성능, 과도 성능, 시작 및 테스트 데이터 분석에 대해 광범위하게 설명합니다. 본 장에는 이러한 설명에 대한 간략한 소개가 포함되어 있습니다. 또한 매개 변수 그룹이 고려하지 않는 2차 '실제 엔진 효과'에 대해서도 설명합니다.
4.1 파라미터 그룹의 중요성
운용 영역 전체에 걸쳐 엔진 성능을 수치로 설명하기 위해서는 많은 변수가 필요합니다. 이는 엔진의 선형 스케일 또는 건공기 이외의 작동 유체를 고려할 때 강조됩니다. 예를 들어, 주어진 설계의 터보젯의 정상 상태 질유량은 나중에 표시된 것과 같이 8개의 매개 변수의 함수입니다.
버킹엄 PI 정리는 많은 수의 매개 변수를 더 적은 수의 무차원 매개 변수 그룹으로 줄입니다. 이러한 그룹에서 모수는 함께 곱해지고 각 모수는 음수 또는 정수가 아닌 일부 지수로 증가합니다. 그에 대한 결과는 엔진 성능에 대한 이해와 그래프 표현을 크게 단순화합니다.
예를 들어 버킹엄 PI 정리는 주어진 터보젯 설계에 대한 질유량에 적용될 수 있습니다. 질유량에 대한 매개변수 그룹은 8개의 매개변수가 아닌 3개의 다른 매개변수 그룹의 함수가 됩니다.
| Inlet mass flow is a function of: | Dimensionless group for inlet mass flow is a function of: |
| 1 Ambient temperature 2 Ambient pressure 3 Flight Mach number 4 Engine rotational speed 5 Engine diameter (scale factor) 6 Gas constant of working fluid 7 Gamma for working fluid 8 Viscosity of working fluid |
1 Dimensionless group for engine speed 2 Flight Mach number 3 Dimensionless group for viscosity (has only a second-order effect, and is often ignored for initial calculations) |
버킹엄 PI 정리는 압축기 및 터빈과 같은 개별 구성 요소에 훨씬 더 쉽게 적용될 수 있습니다. 간단한 예를 들어 두 유동의 혼합된 출구 온도는 유입 흐름과 온도의 비율, 즉 4개의 매개 변수가 아닌 2개의 매개 변수 그룹에 따라 달라집니다.
4.2 파라미터 그룹 및 설명표
4.2.1 파라미터 그룹의 표
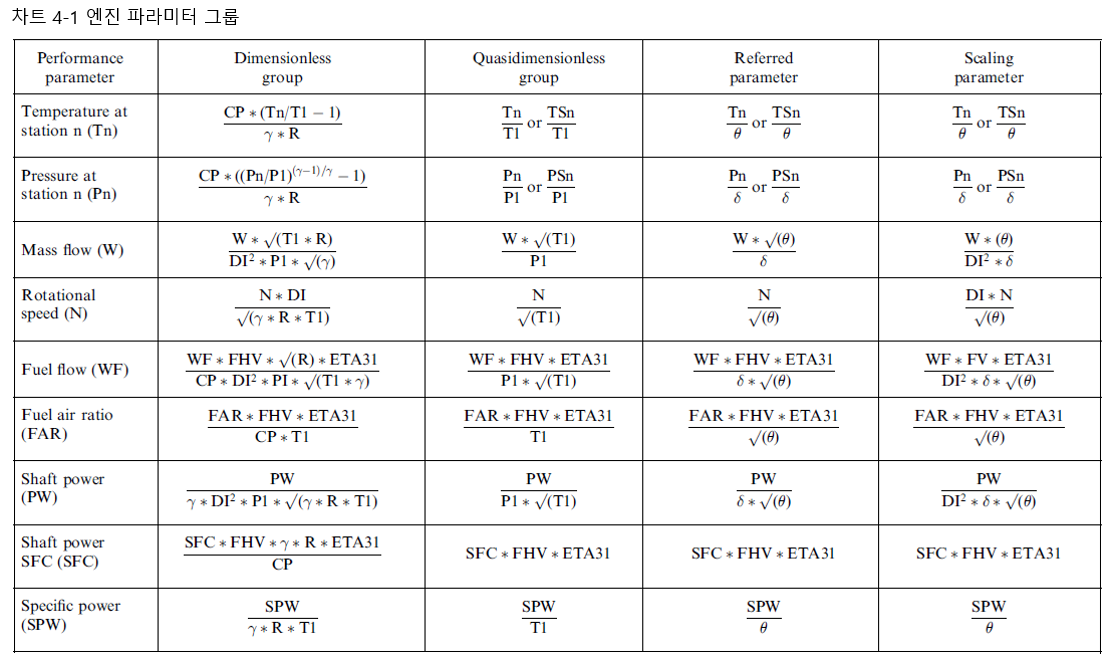
차트 4.1은 전체 엔진 성능에 대한 매개 변수 그룹을 나타내고, 차트 4.2는 구성 요소에 대한 해당 그룹을 나타냅니다. 이러한 차트들은 위에서 논의된 버킹엄 PI 정리를 적용함으로써 첫 번째 원칙으로부터 파생될 수 있습니다.
4.2.2 무차원 그룹
비 차원 그룹 또는 완전 무차원 그룹이라고도 하는 이러한 그룹에는 엔진 선형 척도 및 유체 특성을 포함하여 엔진 또는 구성 요소 성능에 영향을 미치는 모든 변수가 포함됩니다. 이러한 형태는 닫힌 사이클의 헬륨과 같은 다양한 작동 유체를 고려할 때 중요합니다. 차트 4.1과 4.2의 1열에는 주 엔진 및 구성 요소 매개변수에 대한 무차원 그룹이 표시됩니다.
4.2.3 준 차원 그룹
반차원 그룹이라고 하지 않으면, 특정 기체 상수, 감마 및 엔진 직경이 생략됩니다. 이는 건공기를 작동 유체로 사용하는 고정된 선형 스케일의 엔진 또는 구성 요소 설계의 가장 일반적인 상황에 적합합니다. 즉, 작동 조건과 스로틀 설정만 고려해야 합니다. 준 차원이 없는 매개 변수 그룹은 종종 혼란스럽게 비차원이라고 불립니다. 이는 일반적으로 공학적 답변의 유효성에 영향을 미치지는 않지만, 이러한 그룹은 치수를 가지고 있다는 점에 유의해야 합니다. 예를 들어 질량 흐름의 경우 W*sqrt(T/P)의 단위는 kg* sqrt(K/k) Pa*s입니다. 차트 4.1과 4.2의 2열은 주 엔진 및 구성 요소 매개변수에 대한 준 차원 그룹을 보여줍니다.
4.2.4 참조 또는 수정된 그룹
참조되거나 수정된 매개 변수 그룹은 준차원 그룹에 정비례하므로 사용 시 상호 교환할 수 있습니다. 차이는 2장에 정의된 엔진 또는 구성 요소 입구 압력과 온도를 세타(θ)와 델타(δ)로 대체하는 것입니다. 여기서 다음과 같습니다:
델타(δ) - 유입구 압력/101.325 kPa
세타(θ) - 유입구 온도/288.15K
제2장에서 설명한 바와 같이, 전체 엔진 성능은 101.325의 표준 흡기 조건으로 자주 언급됩니다. 참조된 매개 변수는 ISA 해수면 정적 조건에서 기본 매개 변수가 갖는 값을 사용합니다. 단위는 질량 흐름에 대한 kg/s와 같은 기본 매개변수의 단위입니다. 결과 그룹은 차트 4.1 및 4.2의 3열에 표시됩니다.
제2장은 고도, 주변 온도 및 비행 마하 수치에 따른 델타와 세타의 변화를 보여줍니다.
4.2.5 파라미터 그룹의 스케일링
이와 같은 그룹은 작동 유체 속성만 생략된 무차원 그룹입니다. 이러한 엔진의 사용은 새로운 엔진의 개념 설계에 특히 중요합니다. 이를 통해 기존 엔진을 선형적으로 확장하거나 차등적으로 확장된 기존 압축기와 터빈을 일치시키는 성능 효과를 신속하게 평가할 수 있습니다. 차트 4.1 및 4.2의 4열에는 주 엔진 및 구성 요소 매개변수에 대한 스케일링 매개변수 그룹이 나와 있습니다.
4.2.6 파라미터 그룹의 조합
기존 그룹을 결합하여 추가 매개 변수 그룹을 파생할 수 있습니다. 예를 들어, 차트 4.1에 제시된 연료 공기 비율에 대한 그룹은 연료 유량과 엔진 질유량에 대한 그룹을 나누어 얻을 수 있습니다.

'가스터빈(Gas Turbine) 성능 이론' 카테고리의 다른 글
| 4.3 응용 사례 및 4.4 2차 효과 – 정상 상태 성능 (0) | 2023.04.18 |
|---|---|
| 4.3 응용 사례 (0) | 2023.04.16 |
| 3.6 주요 열역학적 파라미터의 상호관계를 보여주는 차트(2) (0) | 2023.04.06 |
| 3.6 주요 열역학적 파라미터의 상호관계를 보여주는 차트(1) (0) | 2023.04.04 |
| 3.4 계산에서 CP와 감마 또는 비 엔탈피와 엔트로피의 사용 및 3.5 기초 및 열역학적 기체 특성에 대한 데이터베이스 (0) | 2023.04.03 |





댓글